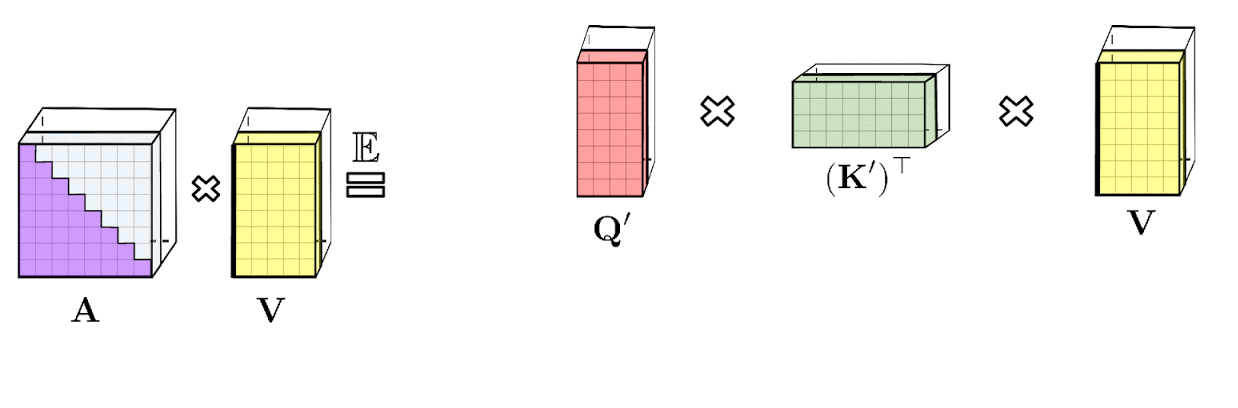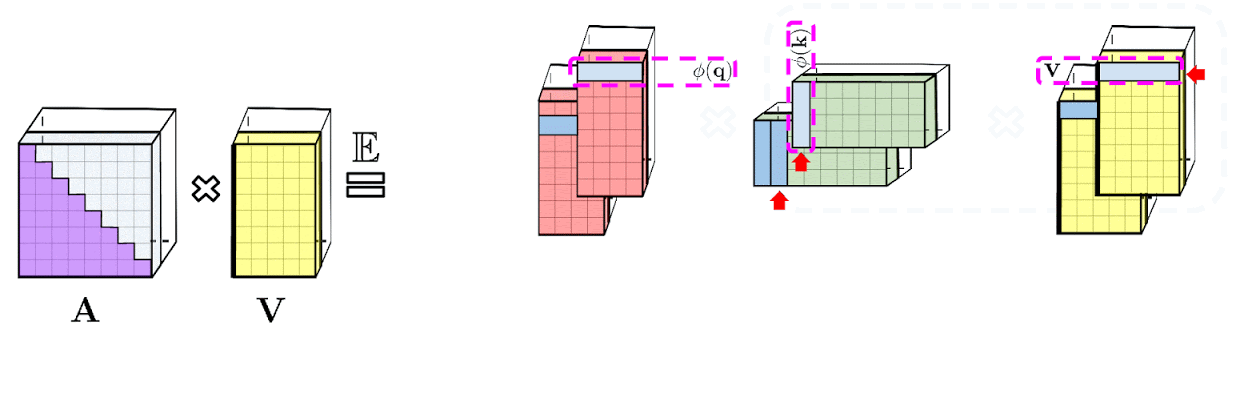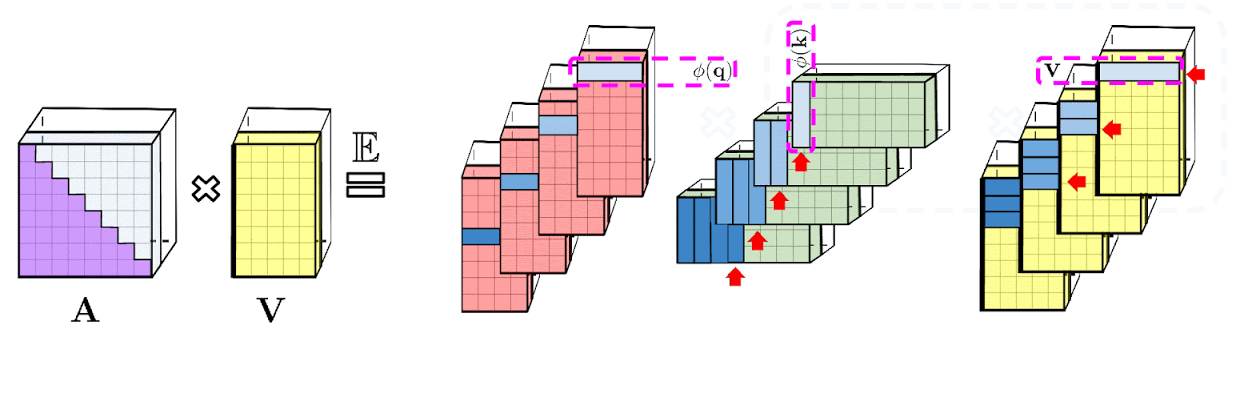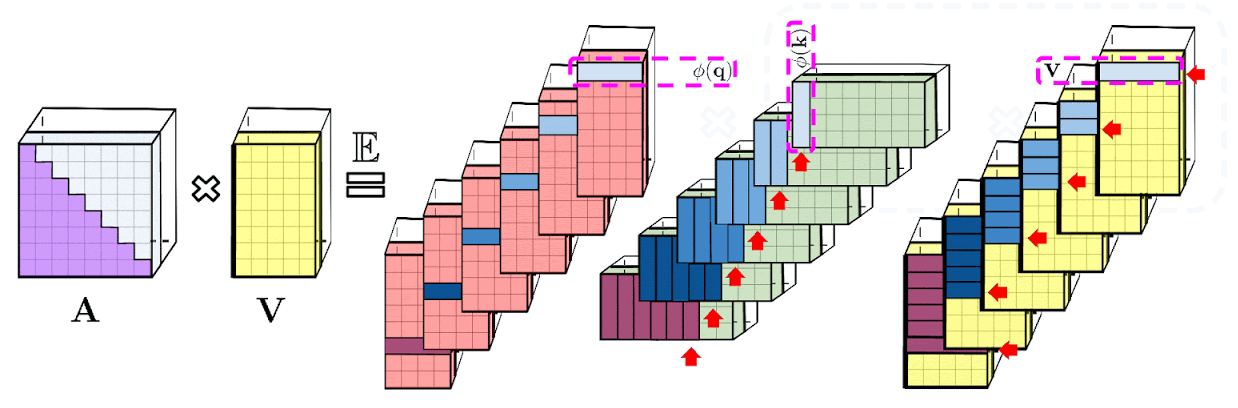
Having looked at google-research’s fast attention tensorflow implementation and corresponding blog post, I was left scratching my head about the causal attention implementation. This post discusses a simpler implementation.
TL;DR
We provide implementations for computing low-rank causal attention equivalent to that discussed in the performer paper. Compared to the original implementation, our implementations:
- are based on a concise mathematical formulation;
- are much shorter (5 lines vs. 47 of the original), making it much easier to reason about;
- do not require custom gradients;
- do not involve python loops over tensors, meaking jit-compilation significantly faster;
- give the same output (within floating point error); and
- run in essentially the same time according to
google-benchmark(after compilation/warm-up).
Operations and test/benchmark scripts are provided in simple-fast-attention.
Theory
The google-ai blog post provides a visualisation of causal attention (included above).
It’s not immediately apparent to me what’s going on here, and looking at the code doesn’t help much.
My implementation takes a different approach. The task is to compute the noncausal numerator $N$, where
$N = \left[(Q K^T) \circ L\right] V$
where $Q$, $K$ and $V$ are the query, key and value matrices used in non-causal fast attention, $L$ is a lower triangular matrix with values of $1$ on and below the diagonal and $\circ$ is the Hadamard product (elementwise product). Noting that $Q$ and $K$ are low-rank (that’s the whole point of performers), we can use the following handy dandy property of Hadamard products (Property 1):
$\left[A \circ \sum_j \mathbf{u}_j \mathbf{v}_j^T\right]\mathbf{x} = \sum_j D(\mathbf{u}_j) A D(\mathbf{v}_j) \mathbf{x}$
where $D(\mathbf{z})$ is the diagonal matrix with diagonal values $\mathbf{z}$. This means we can express our fast causal attention output as
$N = \sum_m D(\mathbf{q}_m) L D(\mathbf{k}_m) V.
where $\mathbf{q}_m$ and $\mathbf{k}_m$ are the $m^\text{th}$ columns of Q and K respectively.
Note it is neither efficient nor necessary to compute any of the new matrices above. $D(\mathbf{k}_m) Z$ is just the scaling of rows of $Z$ by $\mathbf{k}_m$, while $L Z$ is the cumulative sum of $Z$ on the leading dimension. This results in a significantly simpler tensorflow implementation without the need to implement custom gradients or use python loops.
The implementation looks slighty different to the maths above because we compute $D(\mathbf{k}_m) V$ simultaneously for all $m$ and then combine scaling and reduction over $m$ simultaneously using tf.linalg.matvec.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def causal_numerator(qs: tf.Tensor, ks: tf.Tensor, vs: tf.Tensor):
"""Computes not-normalized FAVOR causal attention A_{masked}V.
Args:
qs: query_prime tensor of the shape [L,B,H,M].
ks: key_prime tensor of the shape [L,B,H,M].
vs: value tensor of the shape [L,B,H,D].
Returns:
Not-normalized FAVOR causal attention A_{masked}V.
"""
# rhs = tf.einsum('lbhm,lbhd->lbhdm', ks, vs)
rhs = tf.expand_dims(ks, axis=-2) * tf.expand_dims(vs, axis=-1) # [L,B,H,D,M]
rhs = tf.cumsum(rhs, axis=0)
# return tf.einsum('lbhm,lbhdm->lbhd', qs, rhs)
return tf.linalg.matvec(rhs, qs)
After removing comments and documentation, that’s a 3-line implementation as opposed to the 25 used in the original.
Denominator
The noncausal denominator function is conceptually the same as the numerator except using the ones vector for $V$. Since the first operation involves scaling $V$, we can skip this entirely and just use the keys ks:
1
2
3
4
5
6
7
8
9
10
11
12
def causal_denominator(qs, ks):
"""Computes FAVOR normalizer in causal attention.
Args:
qs: query_prime tensor of the shape [L,B,H,M].
ks: key_prime tensor of the shape [L,B,H,M].
Returns:
FAVOR normalizer in causal attention.
"""
rhs = tf.cumsum(ks, axis=0)
return tf.einsum("lbhm,lbhm->lbh", qs, rhs)
That’s 2 lines compared to 22 in the original.
Benchmarking
Simple and elegant implementations are all well and good, but it’s a rather moot point if performance suffers. Using google-benchmark we can show our implementation compiles significantly faster and is just as performant after warm-up.
Take-aways:
- There isn’t much difference between implementations in terms of computation time
- our implementations warm-up significantly faster
- jit compilation significantly reduces forward time on cpu, but is negligible on gpu
The below is the result of running gbenchmark.py on my fairly old laptop with an NVidia 1050-Ti. v0 is the original implementation, while v1 is my own.
--------------------------------------------------------------
Benchmark Time CPU Iterations
--------------------------------------------------------------
v0_forward-cpu 5403096 ns 364764 ns 1000
v1_forward-cpu 5419832 ns 365650 ns 1000
v0_backward-cpu 268558 ns 238634 ns 2896
v1_backward-cpu 267089 ns 235842 ns 2937
v0_forward-gpu 288531 ns 241580 ns 2874
v1_forward-gpu 285695 ns 238078 ns 2908
v0_backward-gpu 268220 ns 237309 ns 2869
v1_backward-gpu 268324 ns 240429 ns 2751
v0_forward-cpu-jit 299143 ns 271613 ns 2516
v1_forward-cpu-jit 291873 ns 269618 ns 2538
v0_backward-cpu-jit 303150 ns 275359 ns 2483
v1_backward-cpu-jit 303948 ns 276806 ns 2482
v0_forward-gpu-jit 278147 ns 277842 ns 2450
v1_forward-gpu-jit 276128 ns 275956 ns 2523
v0_backward-gpu-jit 256809 ns 256798 ns 2706
v1_backward-gpu-jit 252543 ns 252537 ns 2769
Warmup time for v0_forward-cpu: 6.56445574760437
Warmup time for v1_forward-cpu: 0.1015627384185791
Warmup time for v0_backward-cpu: 22.0670325756073
Warmup time for v1_backward-cpu: 0.08140373229980469
Warmup time for v0_forward-gpu: 6.233572244644165
Warmup time for v1_forward-gpu: 0.028412342071533203
Warmup time for v0_backward-gpu: 22.226712226867676
Warmup time for v1_backward-gpu: 0.051419734954833984
Warmup time for v0_forward-cpu-jit: 6.481787443161011
Warmup time for v1_forward-cpu-jit: 0.05790424346923828
Warmup time for v0_backward-cpu-jit: 24.72081184387207
Warmup time for v1_backward-cpu-jit: 0.09151363372802734
Warmup time for v0_forward-gpu-jit: 8.328083515167236
Warmup time for v1_forward-gpu-jit: 0.08592033386230469
Warmup time for v0_backward-gpu-jit: 24.7033634185791
Warmup time for v1_backward-gpu-jit: 0.12377095222473145
Conclusion
Research is messy. While it’s tempting to think those at google are gods who write things as simply as possible any resulting complexity is inherent to the problem, sometimes simplifications fall through the cracks. In this case we’ve significantly simplified the implementation and drastically improved compilation time without affecting runtime performance. These changes in isolation are unlikely to change the world, but if it makes reasoning about and extending these ideas easier I think they’re well worth doing.
